DAG 简单介绍

Posted on

文章大纲

  • 介绍 DAG 是什么
  • 介绍 DAG 能解决什么问题，有哪些出名的系统是依赖 DAG 的
  • 介绍 DAG 的实现
  • 介绍 DAG 算法场景

DAG 是什么？

DAG（有向无环图）是图论中的一个概念，是由边连接的节点组成的图结构，具有以下几个特性：

  • 有向性：图中的每条边都有方向，即从一个节点指向另一个节点。
  • 无环性：图中不存在环路。换句话说，从任意节点出发沿着边的方向移动，不可能回到起始节点。
  • 路径：在DAG中，可以从一个节点出发，沿着有向边行进到达另一个节点，这条行进轨迹称为路径。
  • 拓扑排序：由于DAG的无环性质，它可以进行拓扑排序，即可以将所有的节点排列成一个线性序列，使得对于任意一条有向边(u, v)，u在序列中都排在v之前。这是DAG的一个重要特性，广泛应用于任务调度、依赖解析等领域。
  • 存在起始节点和终止节点：在DAG中，存在没有入边的节点（入度为0），称为起始节点；存在没有出边的节点（出度为0），称为终止节点。
  • 子图也是DAG：DAG的任何子图也都是有向无环图。
  • 单一路径或多路径：在DAG中，两个节点之间可能存在一条或多条路径，但由于无环性，这些路径之间不会相交。
  • 应用广泛：DAG在计算机科学中应用非常广泛，例如在表达依赖关系、编程中的任务调度、数据处理流程、区块链技术中如以太坊的智能合约执行等。
  • 无法实现负权重环的检测：由于DAG不存在环，因此不适用于需要检测负权重环的算法，如Bellman-Ford算法(求解单源最短路径问题)。

下图存在环状就明显违反了无环要求
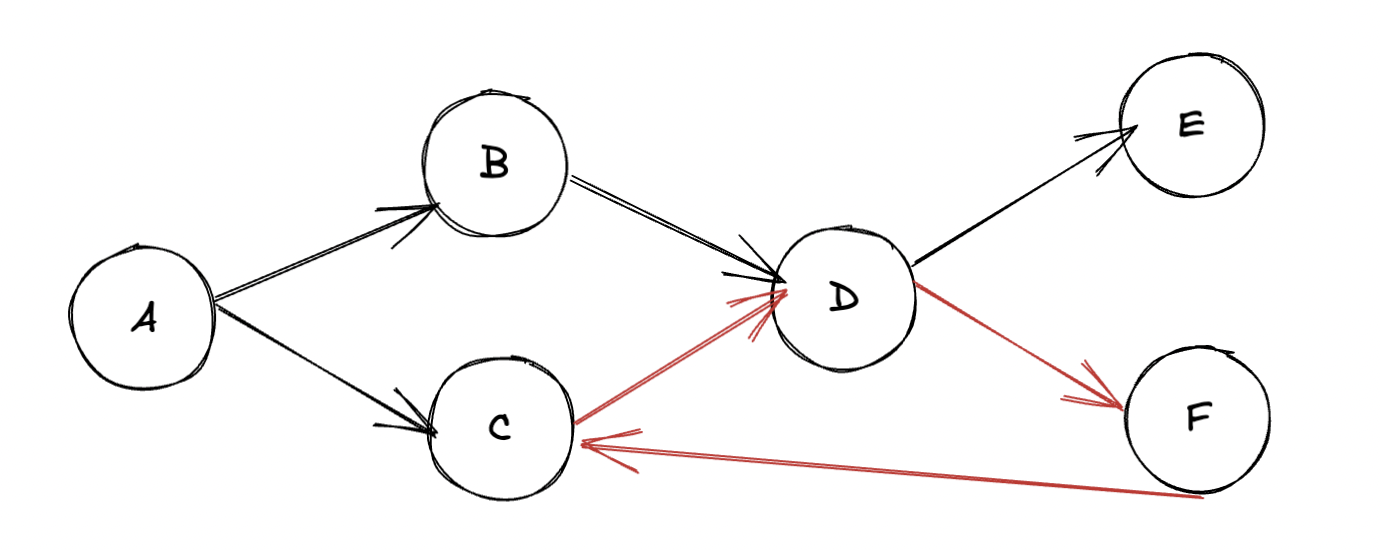
image.png
下图是无向图，不符合 DAG 定义
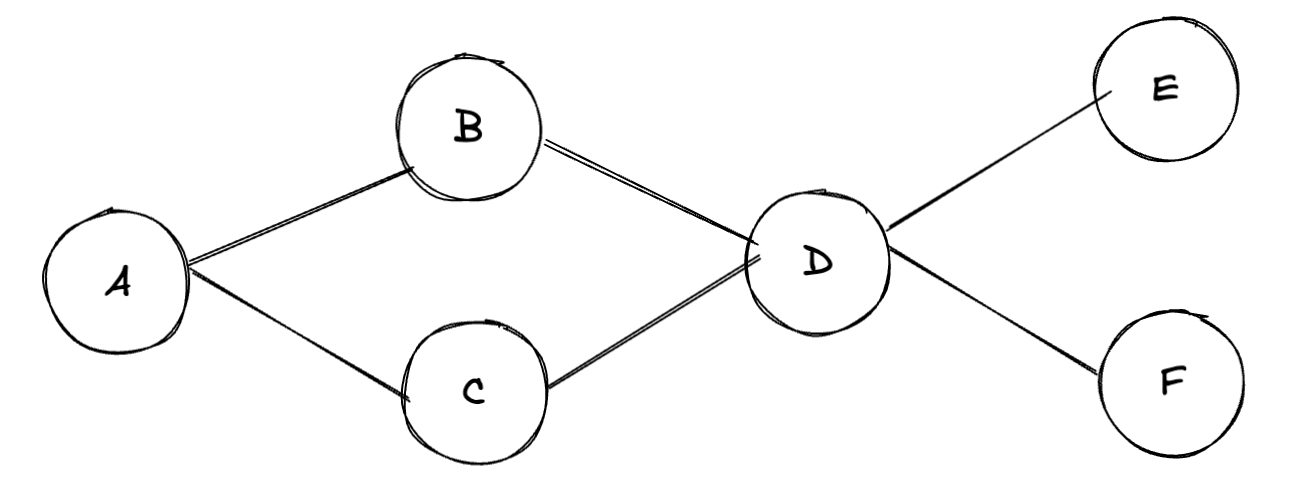
image.png
下图就是符合 DAG 定义的图模型
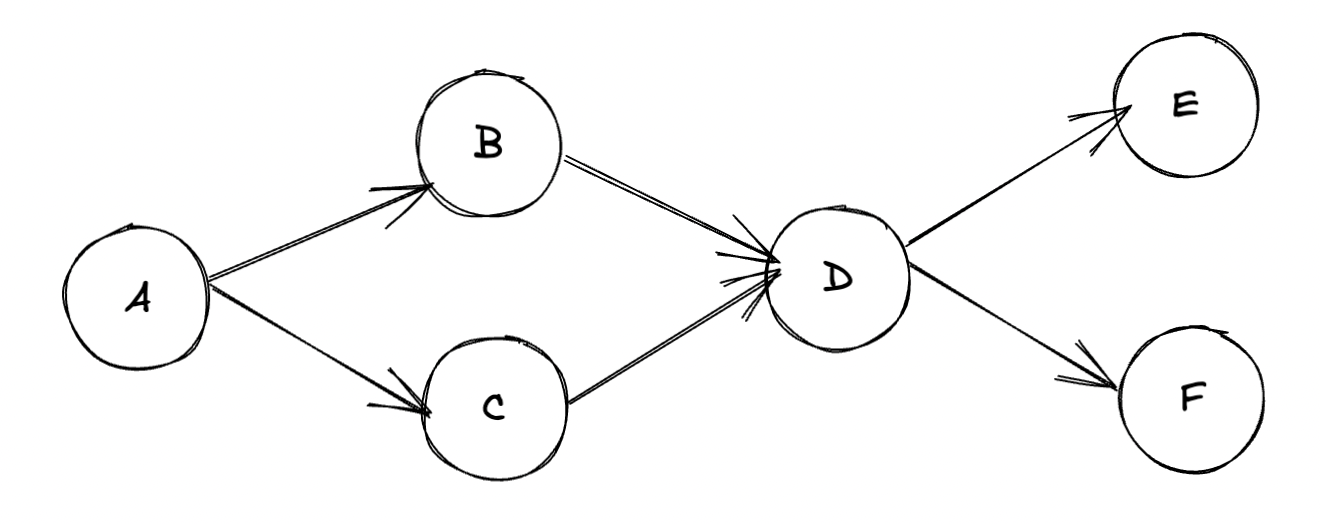
image.png
其中存在一些重要数据模型
Vertex：顶点。A, B, C, D…；一般数据结构模型都是以顶点的方式存储。
Edge：边。A->B，B->D…；表示执行方向。

主要解决什么问题？

  • 数据处理：比如 Flink，通过 DAG 中的顶点表示处理数据的拓扑
  • 调度：常用的调度系统比如 Apache Airflow
  • 系谱或家谱图：它用于展示家族成员之间的关系。将家庭成员用图中的点（顶点）表示，而将亲子关系用连线（边）表示，可以清晰地展示出家族成员之间复杂的血缘关系。这在追踪家族疾病史或研究个人社会背景时很有用。
  • 分布式版本控制系统：这类系统用于管理和记录软件开发过程中各个版本的变化。在这样的系统中，每个软件版本被表示为图中的一个点，而版本之间的衍生关系则通过线来表示，形成了一个有向无环图，有助于开发者理解和管理代码的变更历史。
  • 引用图：在信息科学中，引用图反映了一组文档之间的引用或被引用关系。通过将文档表示为顶点，引用作为边，它能帮助研究人员分析和理解学术论文或文献之间的相互影响和重要性。
  • 贝叶斯网络：它是一种用于表示变量之间依赖关系的概率模型，其中的有向无环图用于直观表达变量之间的条件依赖。该模型在统计学、机器学习和人工智能等领域有广泛的应用，尤其是在进行因果推断和决策支持时非常有用。
  • 数据压缩：在这个应用中，有向无环图用于高效地表示一系列数据，特别是当这些数据序列中存在共享的子序列时。通过将这些共享子序列表示为图中的结构，可以减少存储和传输所需的数据量，从而实现压缩。

DAG 实现调度

Executor 表示执行节点

1
2
3
4
5
public interface Executor {
    boolean execute();
    String getName();
    long getId();
}

Executor 实现类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class Task implements Executor {
    private final long id;
    private final String name;
    private TaskStatus status;

    public Task(long id, String name) {
        this.id = id;
        this.name = name;
        this.status = TaskStatus.INIT;
    }

    @Override
    public boolean execute() {
        System.out.println("Task id: [" + id + "], " + "task name: [" + name +"] is running");
        this.status = TaskStatus.RUNNING;
        // 实际工作
        return true;
    }

    public boolean hasExecuted() {
        return status == TaskStatus.RUNNING;
    }

    @Override
    public long getId() {
        return id;
    }

    @Override
    public String getName() {
        return name;
    }

    public TaskStatus getStatus() {
        return status;
    }

    @Override
    public String toString() {
        return "Task{" + "id=" + id + ", name='" + name + '\'' + ", status=" + status + '}';
    }
}

图实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import com.google.common.base.Preconditions;
import com.google.common.graph.GraphBuilder;
import com.google.common.graph.MutableGraph;

import java.util.Set;
import java.util.stream.Collectors;

public class Digraph {
    // 借助 guava 来构成图
    private final MutableGraph<Executor> graph;
    private Executor startTask = null;

    public Digraph() {
        graph = GraphBuilder.directed().build();
    }

    // 添加任务节点
    public void addVertex(Executor task, Executor prevTask) {
        graph.addNode(task);
        if (prevTask != null) {
            Preconditions.checkArgument(startTask != null);
            graph.putEdge(prevTask, task);
        } else {
            startTask = task;
        }
    }

    // 返回起始任务，可以通过 inDegree 判断但是需要遍历所有 nodes
    public Executor getStartTask() {
        return startTask;
    }

    // 获取后续可以执行的任务
    public Set<Executor> getNextTasks(Executor task) {
        Set<Executor> successors = graph.successors(task);
        // 仅入度为 1 的才具备执行条件，表示前置任务完成
        return successors.stream().filter(v -> graph.inDegree(v) == 1).collect(Collectors.toSet());
    }

    // 如果成功了需要删除节点，减少后续节点的入度，当一个任务依赖多个节点完成时这是判断的依据
    public void success(Executor task) {
        graph.removeNode(task);
    }

    // 是否是结束节点
    public boolean isEnd(Executor task) {
        return graph.outDegree(task) == 0;
    }

}

调度实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Scheduler {
    public void schedule(Digraph digraph) {
        Executor startTask = digraph.getStartTask();
        if (startTask == null) {
            System.out.println("No more tasks to execute");
            return;
        }
        Set<Executor> readyTasks = new HashSet<>();
        readyTasks.add(startTask);
        while (true) {
            Set<Executor> nexts = new HashSet<>();
            boolean isEnd = true;
            // 实际执行可以并发执行，并发需要确保下面操作都是并发安全的
            for (Executor task : readyTasks) {
                if (task.execute()) {
                    System.out.println("Task " + task.getName() + " is executed");
                    nexts.addAll(digraph.getNextTasks(task));
                    isEnd = isEnd && digraph.isEnd(task);
                    digraph.success(task);
                }
            }
            if (isEnd) {
                break;
            }
            readyTasks = nexts;
        }
    }
}

验证

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public static void main(String[] args) {
    /**
     *   -> 2 -> 4 ->
     * 1              6
     *   -> 3 -> 5 ->
     */
    Digraph digraph = new Digraph();
    Task task1 = new Task(1L, "task1");
    Task task2 = new Task(2L, "task2");
    Task task3 = new Task(3L, "task3");
    Task task4 = new Task(4L, "task4");
    Task task5 = new Task(5L, "task5");
    Task task6 = new Task(6L, "task6");
    digraph.addVertex(task1, null);
    digraph.addVertex(task2, task1);
    digraph.addVertex(task3, task1);
    digraph.addVertex(task4, task2);
    digraph.addVertex(task5, task3);
    digraph.addVertex(task6, task3);
    digraph.addVertex(task6, task4);
    Scheduler scheduler = new Scheduler();
    scheduler.schedule(digraph);
}

Task id: [1], task name: [task1] is running
Task task1 is executed
Task id: [2], task name: [task2] is running
Task task2 is executed
Task id: [3], task name: [task3] is running
Task task3 is executed
Task id: [5], task name: [task5] is running
Task task5 is executed
Task id: [4], task name: [task4] is running
Task task4 is executed
Task id: [6], task name: [task6] is running
Task task6 is executed

与 DAG 相关算法

拓扑排序（Topological Sorting）

拓扑排序是将有向无环图的顶点排成一个线性序列，使得对图中的任意两个顶点 u 和 v，若存在边 u -> v，则 u 在这个序列中出现在 v 之前。常用的拓扑排序算法有 Kahn 算法和 DFS（深度优先搜索）算法。

最短/最长路径问题

在 DAG 中，可以使用动态规划方法求解单源最短路径或最长路径问题，这通常涉及先进行拓扑排序，然后在排序后的顺序中依次计算每个顶点的最短/最长路径长度。

动态规划（Dynamic Programming）

DAG 通常与动态规划问题联系紧密，因为许多动态规划问题可以表示为 DAG，其中每个顶点代表一个状态，而边代表从一个状态到另一个状态的转换。

图割（Graph Cuts）

在图像处理、计算机视觉和网络流等领域中，经常需要找到图的割，将图分割成不相交的子集。最小割问题是找到一种边的分割方式，使得割的权重最小，并且分割后图的两个子集满足某些特定的条件。

强连通分量（Strongly Connected Components）

强连通分量是有向图的最大子图，在该子图中，任意一对顶点都是相互可达的。Kosaraju算法、Tarjan算法和Gabow算法是求解强连通分量的几种经典算法。

网络流问题（Network Flow）

最大流问题是网络流问题的一种，用于寻找在保留容量限制的前提下，从源点到汇点的最大可能流量。Ford-Fulkerson 算法和 Edmonds-Karp 算法是解决最大流问题的著名算法。

路径枚举

在某些情况下，我们可能需要列举 DAG 中从一个顶点到另一个顶点的所有路径。这可以通过回溯法结合深度优先搜索（DFS）来实现。

传递闭包（Transitive Closure）

传递闭包是图的一个属性，表示图中顶点之间的可达性。在 DAG 中计算传递闭包可以使用 Floyd-Warshall 算法或者通过深度优先搜索（DFS）的变体来完成。

参考

Practical Applications of Directed Acyclic Graphs
Introduction to Directed Acyclic Graph
「LeetCode」拓扑排序系列（一）
十分钟讲清楚IOTA和DAG
用可替代区块链的DAG实现智能合约